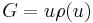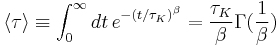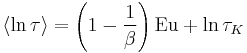Stretched exponential function

The stretched exponential function is a generalization of the exponential function with one additional parameter, the stretching exponent β:

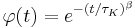$\varphi (t) = e^{ - \left( {t /\tau_K } \right)^\beta }$ .

In most applications, it is meaningful only for arguments t between 0 and +∞. With β=1, the usual exponential function is recovered. With β between 0 and 1, the graph of φ(t) versus log(t) is characteristically stretched, whence the name of the function.

The compressed exponential function (with β>1) has less practical importance, with the notable exception of β=2, which gives the normal distribution.

In mathematics, the stretched exponential is also known as the complementary cumulative Weibull distribution. Furthermore, the stretched exponential is the characteristic function (basically the Fourier transform) of the Lévy symmetric alpha-stable distribution.

In physics, the stretched exponential function is often used as a phenomenological description of relaxation in disordered systems. It was first introduced by Rudolf Kohlrausch in 1854 to describe the discharge of a capacitor;^[1] therefore it is also called the Kohlrausch function. In 1970, G. Williams and D.C. Watts used the Fourier transform of the stretched exponential to describe dielectric spectra of polymers;^[2] in this context, the stretched exponential or its Fourier transform are also called the Kohlrausch-Williams-Watts (KWW) function.

1 Distribution function
2 Mean relaxation time
3 Higher moments
4 Fourier Transform
5 History and further applications
6 References
7 Further reading
8 External links

Distribution function

In some fields of physics, apparent stretched exponential behaviour is often motivated as a linear superposition of simple exponential decays. This requires a nontrivial distribution of relaxation times, ρ(u), which is implicitly defined by

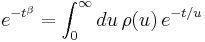$e^{ - t^\beta} = \int_0^\infty du\,\rho(u)\, e^{-t/u}$ .

Alternatively, a distribution

$G=u \rho (u)\,$

is used.

ρ can be computed from the series expansion:^[3] 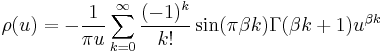$\rho (u ) = -{ 1 \over {\pi u }} \sum\limits_{k = 0}^\infty {{( - 1)^k } \over {k!}}\sin (\pi \beta k)\Gamma (\beta k %2B 1) u^{\beta k }$

Figure 2 shows the same results plotted in both a linear and a log representation. The curves converge to a Dirac delta function peaked at u=1 as β approaches 1, corresponding to the simple exponential function.

Figure 2. Linear and log-log plots of the stretched exponential distribution function 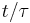$G$ vs $t/\tau$

for values of the stretching parameter β between 0.1 and 0.9.

Mean relaxation time

Following the usual physical interpretation, we interpret the function argument t as a time. The area under the curve φ(t) is therefore interpreted as a mean relaxation time. One finds

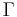$\langle\tau\rangle \equiv \int_0^\infty dt\, e^{ - \left( {t /\tau_K } \right)^\beta } = {\tau_K \over \beta }\Gamma ({1 \over \beta })$

where $\Gamma$ is the gamma function. For exponential decay, $\langle\tau\rangle=\tau_K$ is recovered.

Higher moments

The higher moments of the stretched exponential function are:^[4]

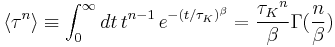$\langle\tau^n\rangle \equiv \int_0^\infty dt\, t^{n-1}\, e^{ - \left( {t /\tau_K } \right)^\beta } = {{\tau_K }^n \over \beta }\Gamma ({n \over \beta })$ .

They are closely related to the moments of the distribution of simple-exponential relaxation times,

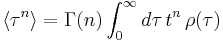$\langle\tau^n\rangle = \Gamma(n) \int_0^\infty d\tau\, t^{n}\, \rho(\tau)$ .

The first logarithmic moment of the distribution of simple-exponential relaxation times is

$\langle\ln\tau\rangle = \left( 1 - { 1 \over \beta } \right) {\rm Eu} %2B \ln \tau_K$

where Eu is the Euler constant.^[5]

Fourier Transform

To describe results from spectroscopy or inelastic scattering, the sine or cosine Fourier transform of the stretched exponential is needed. It must be calculated either by numeric integration, or from a series expansion.^[6] For practical purposes, the Fourier transform may be approximated by the Havriliak-Negami function.^[7]

History and further applications

As said in the introduction, the stretched exponential was introduced by the German physicist Rudolf Kohlrausch in 1854 to describe the discharge of a capacitor (Leyden jar) that used glass as dielectric medium. The next documented usage is by Friedrich Kohlrausch, son of Rudolf, to describe torsional relaxation. A. Werner used it in 1907 to describe complex luminescence decays; Theodor Förster in 1949 as the fluorescence decay law of electronic energy donors.

Outside condensed matter physics, the stretched exponential has been used to describe the removal rates of small, stray bodies in the solar system,^[8] and the diffusion-weighted MRI signal in the brain.^[9]

References

^ Kohlrausch, R. (1854). "Theorie des elektrischen Rückstandes in der Leidner Flasche". Annalen der Physik und Chemie (Poggendorff) 91: 56–82, 179–213. http://gallica.bnf.fr/ark:/12148/bpt6k15176w.pagination. .
^ Williams, G. and Watts, D. C. (1970). "Non-Symmetrical Dielectric Relaxation Behavior Arising from a Simple Empirical Decay Function". Transactions of the Faraday Society 66: 80–85. doi:10.1039/tf9706600080. .
^ Lindsey, C. P. and Patterson, G. D. (1980). "Detailed comparison of the Williams-Watts and Cole-Davidson functions". Journal of Chemical Physics 73: 3348–3357. doi:10.1063/1.440530. . For a more recent and general discussion, see Berberan-Santos, M.N., Bodunov, E.N. and Valeur, B. (2005). "Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential)". Chemical Physics 315: 171–182. doi:10.1016/j.chemphys.2005.04.006. .
^ I.S. Gradshteyn (И.С. Градштейн), I.M. Ryzhik (И.М. Рыжик); Alan Jeffrey, Daniel Zwillinger, editors. Table of Integrals, Series, and Products, fourth edition. Academic Press, 1980. Integral 3.478.
^ Zorn, R. (2002). "Logarithmic moments of relaxation time distributions". Journal of Chemical Physics 116: 3204–3209. doi:10.1063/1.1446035.
^ Dishon et al. 1985.; Wuttke http://arxiv.org/abs/0911.4796v1
^ Alvarez, F., Alegría, A. and Colmenero, J. (1991). "Relationship between the time-domain Kohlrausch-Williams-Watts and frequency-domain Havriliak-Negami relaxation functions". Physical Review B 44: 7306–7312. doi:10.1103/PhysRevB.44.7306.
^ Dobrovolskis, A., Alvarellos, J. and Lissauer, J. (2007). "Lifetimes of small bodies in planetocentric (or heliocentric) orbits". Icarus 188: 481–505. doi:10.1016/j.icarus.2006.11.024.
^ Bennett, K. et al. (2003). "Characterization of Continuously Distributed Water Diffusion Rates in Cerebral Cortex with a Stretched Exponential Model". Magn. Reson. Med. 50: 727–734. doi:10.1002/mrm.10581.

External links

J. Wuttke: libkww C library to compute the Fourier transform of the stretched exponential function